I've always been interested in biologically-inspired machine learning models. My first first flirtation with bio-inspired ML was nearly 8 years ago. Named “Distributed Neuron”, the goal was to build a clustered machine learning algorithm inspired by actual growth patterns of neurons (neurotropic factors, signaling gradients, etc), instead of the relatively sterile and rigid “neural networks” that were popular at the time.

There's not much left of that project, other than a few saved snapshots on the Wayback Machine where I talk about it on my now-defunct neuroscience blog. I also found a few old video recordings on yourtube, showing “neuron activations” in 3D:

Suffice to say, Distributed Neuron was a bit ambitious for my younger self. I've toyed with less complex projects in the intervening 8 years, but it's mostly been a slow simmer always in the back of my mind. Recently, I stumbled across an interesting paper detailing a neurally-inspired cellular automata called CoDi-1Bit.¹

The CoDi-1Bit system (CoDi from now on) was designed to be simple, minimal and computationally compact, primarily so that it could easily be expressed on an FPGA. The system was used to rapidly evolve and evaluate neural networks in silico, with the goal of building discrete modules that perform specific functionality: timers, pattern detectors, Hubel-Wiesel Line Motion detectors, etc ^{2 3}

The ultimate goal was to control a robotic cat in real-time, hence the choice of FPGAs (fast evolution and fast real-time control).

CoDi makes a lot of generalizations about the behavior of neurons. Which is not surprising; anything which distills a complex process like neural signaling into a cellular automata is bound to be a poor facsimile of the real thing.

But despite the shortcomings, the system seems very interesting. Best I can tell, the research on CoDi ended in 2001 when the research division was shut down, having failed to produce the aforementioned robotic cat.

So hey, this sounds like a fun side project. Let's revive CoDi with cluster computing instead of FPGA and see what happens. :)

CoDi-1Bit System

The CoDi system is a cellular automata (CA) which is designed to, roughly, mimic neurons. A handful of “neuron bodies” are seeded onto the CA grid. The grid then undergoes a series of “growth” iterations. First, each neuron will sprout two “axons” into adjacent cells (each opposite the other, e.g north and south). Next, the neuron body will sprout two “dendrites” in the other adjacent cells (e.g. west and east). That ends the first iteration.

Note: This is actually a bit of a simplification, since the original Codi system used three-dimensional grids instead of 2D grids. But I'm only working with 2D, so further explanations will assume that.

During the next and all subsequent iterations, each individual grid cell manages its own growth. It does this by consulting a “chromosome” that is overlaid across the entire grid. This chromosome is nothing more than a set of instructions: grow straight, turn left, turn right, split right + grow straight, etc. At each step, the grid cell will look at the underlying chromosomal instruction and perform the action.

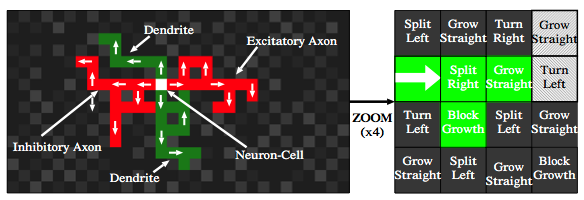
Importantly, the newly grown cell maintains it's lineage. A dendrite will grow more dendritic cells, axons grow more axonal cells. Also important is that each grid cell maintains a pointer in the direction that it just grew from. That means you could, for example, pick any dendrite cell and follow the pointers back to the original neuron body. This is how the signaling network is setup.

Growth will not “overwrite” a pre-existing body/axon/dendrite, and so the growth phase will eventually come to a close when all empty cells are used and/or the active cells have no where else to grow. The signaling phase would then begin, but we'll save that explanation for a future article.

The overlaid chromosome is a fairly clever trick. When I was building Distributed Neuron, each individual neuron maintained it's “preferences” for growth: how attractive is X growth factor, how repellent is Y, what's my branching factor, etc. This required a relatively large amount of memory for each cell, and required axon/dendrites to point back to their originating neuron body in some fashion.

In contrast, growth in Codi is basically spelled out in the grid itself, using a mere 4 bits. And since each cell points back the way it came, no individual cell needs to store it's originating source…you just follow the trail backwards.

There are some other nice benefits. For example, evolutionary changes are intrinsically local. A mutation to one position in the chromosome will affect at most a few neurons, which will help genetic algorithms tweak without completely destroying stability.

I'm not completely sold on the idea, since it is very restrictive. But it does seem like an interesting base to work off of. We'll talk more about the chromosome in the future when looking at the genetic algorithm aspects.

Cajal

Named after Santiago Ramón y Cajal⁵, Cajal can currently create an arbitrarily sized grid, grow a Codi-esque network, inject signal and watch the neurons fire. Fair warning: the code is a complete mess in most places, and an unmitigated disaster in others. A proper Readme and refactoring will happen soon :)

Today I want to look at the lowest level of Cajal: the Cell. The world grid is divided into a vector of Pages, and each Page is composed of a vector of Cells. Due to the heritage of Codi, each cell is represented by a single u32:

#[derive(Clone, Copy, Debug)]
pub struct Cell {
    data: u32
}

All the information about a particular spot on the grid is encoded in these 32 bits: chromosomal information, directionality, cell type, firing threshold, etc. To access these values, we setup a series of masks over the u32:

const CELL_TYPE_MASK: u32  = 0b0000000000_00_00_00_000000_0000_0_00_111;  // ---
const GATE_MASK: u32            = 0b0000000000_00_00_00_000000_0000_0_11_000;  // | Growth Phase
const STIM_MASK: u32            = 0b0000000000_00_00_00_000000_0000_1_00_000;  // |
const CHROMO_MASK: u32        = 0b0000000000_00_00_00_000000_1111_0_00_000;  // ---

const STRENGTH_MASK: u32   = 0b0000_000000_00_00_00_000000_1111_0_00_000;  // ---
const THRESHOLD_MASK: u32 = 0b0000_000000_00_00_00_111111_0000_0_00_000;  // | Signal Phase
const POT_1_MASK: u32         = 0b0000_000000_00_00_11_000000_0000_0_00_000;  // |
const POT_2_MASK: u32         = 0b0000_000000_00_11_00_000000_0000_0_00_000;  // |
const POT_3_MASK: u32         = 0b0000_000000_11_00_00_000000_0000_0_00_000;  // |
const SIGNAL_MASK: u32       = 0b0000_111111_00_00_00_000000_0000_0_00_000;  // ---

The first three bits hold the cell type, the next two hold the Gate (the “pointer” back towards the cell we grew from), a single bit holds if we are a stimulatory or inhibitory axon, the next four hold the chromosome information, etc.

Some bits are exclusive values. For example, the Gate bits represent one of four cardinal directions (north, south, east, west). Since a gate can only point in one direction at a time, we can express those four variants in just two bits.

Other's are bit flags. For example, a chromosome can point to north, south, east, west, or any combination of the directions. Which means we need four bits to hold all the possible values.

Paired with these masks are a set of offsets. These make it easier to define enums over the u32; we can shift by the offset instead of including empty bits in each enum definition explicitly.

const CELL_TYPE_OFFSET: u8  = 0;
const GATE_OFFSET: u8            = 3;
const STIM_OFFSET: u8            = 5;
const CHROMO_OFFSET: u8        = 6;

const STRENGTH_OFFSET: u8    = 6;
const THRESHOLD_OFFSET: u8  = 10;
const POT_1_OFFSET: u8          = 16;
const POT_2_OFFSET: u8          = 18;
const POT_3_OFFSET: u8          = 20;
const SIGNAL_OFFSET: u8        = 22;

Now we can start defining the enums that will sit on top of this u32, so we can work with well-typed enums instead of shifting bits around all the time. Let's look at CellType, the enum that controls what the cell holds:

enum_from_primitive! {
    #[derive(Debug, PartialEq, Copy, Clone)]
    pub enum CellType {
        Empty = 0b000,
        Body = 0b001,
        Axon = 0b010,
        Dendrite = 0b011
    }
}

The enum itself is fairly unremarkable: defined in binary for easier reading, it lists four different cell types. It also derives some useful traits we'll need later. But what's this enum_from_primitive macro?

The macro is from the enum_primitive crate, and generates a num::FromPrimitive implementation for CellType. This makes it simpler to do operations such as get_cell_type():

pub fn get_cell_type(&self) -> CellType {
    match CellType::from_u32((self.data & CELL_TYPE_MASK) >> CELL_TYPE_OFFSET) {
        Some(ct) => ct,
        None => unreachable!()
    }
}

The snippet takes our 32 bits of data, AND's it with the CellType mask (so that we are only concerned with the CellType data, and not the other components), shifts it the appropriate offset and then converts the resulting integer into a nicely typed enum. The alternative is an exhaustive match, which would work fine but requires more typing :)

There is, unsurprisingly, a set_cell_type() method. It's essentially the inverse of the above function:

pub fn set_cell_type(&mut self, cell_type: CellType) {
    self.data = (self.data & !CELL_TYPE_MASK) | ((cell_type as u32) << CELL_TYPE_OFFSET);
}

We take our u32, AND it with the inverse of the mask, then OR it with our desired cell type (shifted by the appropriate offset). This will replace the existing bits with the new cell type.

The rest of the Cell definitions are similar for the various components (chromosome, signal threshold, etc). There are also a variety of utility traits, such as Not for CellType, which simply “inverts” the cell type:

impl Not for CellType {
    type Output = CellType;

    fn not(self) -> CellType {
        match self {
           CellType::Body => CellType::Empty,
           CellType::Empty => CellType::Body,
           CellType::Axon => CellType::Dendrite,
           CellType::Dendrite => CellType::Axon,
        }
    }
}

This is convenient, since we often want to do the opposite behavior for axons and dendrites. Implementing Not allows us to say if target == !cell_type for example. The other components of the cell implement similar convenience traits, such as BitAnd, BitOr, From, Rand, etc

Z-ordering Cells

One of the main benefits of Codi is that the representation is compact. The state of each grid cell is encoded in just 32 bits (originally 16, but I expanded it to include some more information). Which means Codi plays nicely with CPU pre-fetching… assuming we lay it out correctly.

The naive way to arrange the cells would be something like row-major order: (0,0) -> (0,n), followed by (1,0) -> (1,n), etc. The problem is that cellular automata need to access their immediate neighborhood on most operations. When evaluating a cell at (10,10), we will likely need to inspect (10,11), (10,9), (9,10), and (11,10). If stored in row-major order, the north and south cells are likely to be in a different cache line, causing a cache-miss and slowing down the whole computation since we have to trek back to main memory.

Instead, the cells are arranged in Z-Order, using a Morton code.

A Z-Order or Morton Code is a space-filling curve which happens to place nearby positions in the cartesian plane close together in the 1-dimensional sequence. That means when evaluating a cell, it's likely that most or all of it's neighbors (in the cartesian plane) will be located nearby in memory… hopefully close enough to be in the same cache line and avoid a miss.

To facilitate this, there is a zorder module which provides two simple functions to convert to/from zordering (credit to Fabian Giesen for the article and implementation base the functions are based on).

This makes it trivial to swap between the different representations depending on what we need. For example, given an (x,y) coordinate pair and a direction of travel, we can calculate the “target” position in that direction of travel:

fn calc_target(x: u32, y: u32, direction: Gate) -> u32 {
    match direction {
        Gate::North => zorder::xy_to_z(x, y + 1),
        Gate::South => zorder::xy_to_z(x, y - 1),
        Gate::East => zorder::xy_to_z(x + 1, y),
        Gate::West => zorder::xy_to_z(x - 1, y),
    }
}

Or, given an (x,y) pair, we can determine which cell to operate on:

pub fn add_change(&mut self, x: u32, y: u32, cell: Cell) {

    let cell_type = cell.get_cell_type();
    let target = zorder::xy_to_z(x, y);

    if self.cells[target].get_cell_type() == CellType::Empty {
        self.changes.insert(target, Page::create_change(cell_type));
    }
}

And of course, we can go the other direction too. When looping over the list of “active” cells to process, we often need to convert their index position into real (x,y) coordinates:

for index in self.active.iter() {
    let (x, y) = zorder::z_to_xy(index);

    let cell_type = cells[index].get_cell_type();

    for direction in CARDINAL_DIRECTIONS {
        if cells[index].get_chromosome().contains(Chromosome::from(*direction)) {
            let change = Page::process_chromosome_direction(*direction, x, y, cell_type);

            Page::persist_change(&mut self.changes, &mut self.remote_changes, change);
        }
    }
}

Simple, but effective and relatively transparent once you get used to working with the conversion.

Conclusion

That's all for now. A relatively boring article, truth be told, but it was difficult to talk about the interesting aspects of Cajal without laying down a base of history and background. Hopefully future articles will be more interesting, talking about how signaling works, the parallel execution of computation units with Rayon, performance tuning, genetic algorithm evolution and eventually clustered computing.